Задания по математике для 7 класса

1. Определите, какое из чисел больше:

Решение: Так как

и, аналогично,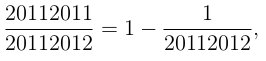 
то достаточно сравнить числа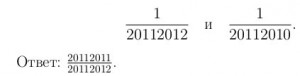 

2. Двоечник Вася вырвал из учебника все страницы, в номерах которых есть цифра 2. Оказалось, что он вырвал ровно половину всех страниц. Известно, что в учебнике было больше
100, но меньше 300 страниц. Сколько страниц было в учебнике?

Решение:

В первой сотне Вася вырвал 15 пар страниц (листов) из 50-ти:
(1, 2), (11, 12), (19, 20), (21, 22), . . . , (29, 30),
(31, 32), (41, 42), (51, 52), . . . , (91, 92).
Осталось 35 листов, разница в 20 листов. Во второй сотне все го 16 пар вырванных (добавляется пара (199, 200)), это меньше 20-ти, значит перевес между оставляемыми и вырваемыми листами будет сохранятся на протяжении всей второй сотни.
Итак, в книге больше 200 страниц. При этом из первых 200 страниц вырвали 16 + 15 = 31 лист. Разница между оставшимися и вырванными листами в двух первых сотнях равна
38. Все листы со страницами 2xx будут вырываться, для сокращения разности нужно вырвать 38 листов, т.е. 76 страниц. Итак, в книге было 276 страниц.
Ответ: 276.

3. Найдите наименьшее четное число с суммой цифр, равной 2011.

Решение: 599 . . . 998. Всего 222 девятки.

4. Найдите все простые числа x, y, z, для которых справедливо равенство

z = 1991 + 5 · 2^y .

Решение: 

Число z — простое и больше 1991. Поэтому z нечетное, откуда x четное, и, следовательно, x = 2. Итак, z = 1991 + 5 · 2^y .
Рассматривая степени двойки, видим, что 2^2k − 1 = 4^k − 1 делится на 3. Поэтому при нечетном y
z = 1992 + 3 · 2^y + 2^y+1 − 1 делится на 3. Следовательно y четно, и y = 2, а z = 2011.
Ответ: x = 2, y = 2, z = 2011.

5. Найдите хотя бы одну тройку (x, y, z) натуральных чисел такую, что

2(x + y + z) = xy + yz + zx − 2011.

Решение: Попробуем x = 1. Тогда 2(1 + y + z) = y + yz + z − 2011, откуда 2014 = yz − y − z + 1 = (y − 1)(z − 1). Ответ: x = 1, y = 2, z = 2015.