Задания по математике для 9 класса

1. Поверхность деревянного куба окрасили в красный цвет. После этого куб распили на 1000 одинаковых кубиков. Вычислите, сколько из этих кубиков имеют ровно две окрашенные грани.
Решение: Все такие кубики были на ребре, но не в вершинах куба.
Ребер 12, на каждом ребре 10 − 2 = 8 таких кубиков. Всего 12 · 8 = 96. Ответ: 96.

2. Докажите неравенство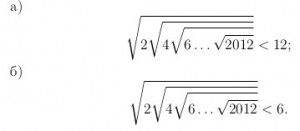 
Решение: Так как 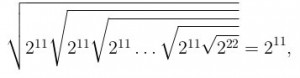 то  Далее,  поэтому Аналогично 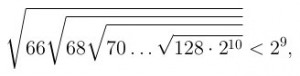и так добираемся до  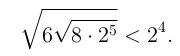Значит

3. Докажите, что при a > 3 уравнение 2(x + y + z) = xy + yz + zx + a не имеет решений в натуральных числах x, y, z.
Решение: Так как
xy + 1 ≥ x + y, yz + 1 ≥ y + z, zx + 1 ≥ z + x, то xy + yz + zx + a > xy + yz + zx + 3 ≥ 2(x + y + z).

4. Докажите, что последовательность an = 2011 + 6033n содержит бесконечно много квадратов натуральных чисел.
Решение: a_n = 2011(1 + 3n). Пусть A = 2011² (3k + 1)² , где k — произвольное натуральное число. Тогда A = 2011(3n + 1) с некоторым целым n, т.е. A = a_n .

5. Площадь равнобедренного прямоугольного треугольника ABC равна 1. Найдите площадь треугольника, образованного основаниями биссектрис треугольника ABC.
Примечание. Площадь S произвольного треугольника может быть вычислена по формулам: S = ah/2 или S = ab sin γ/2 , где a и b — стороны треугольника; h — высота, опущенная на сторону a; а γ — угол между сторонами a и b.
Решение: Пусть основания биссектрис A₁ , B₁ и C₁ , ∠ACB = 90^o . По свойству биссектрис |AB₁| : |CB₁| = |AB| : |CB| = √ 2, и, следовательно,  Тогда  Аналогично  В итоге