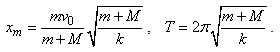Задания по физике для 10 класса
Задача 1. Двигатель запускаемого с земли реактивного снаряда массой m работает время τ, создавая постоянную по величине и направлению силу тяги F и обеспечивая прямолинейное движение снаряда под углом α к горизонту. Определите высоту, на которой прекращается работа двигателя.
Решение: На снаряд во время полета действует сила тяжести и сила тяги F, направленная под углом β к горизонту (см.рис.). Равнодействующая этих сил Fp направлена под углом α к горизонту и сообщает снаряду ускорение а. На рис. видно, что и . После возведения в квадрат и сложения этих уравнений получим: . Решая квадратное уравнение, находим . Ускорение , его вертикальная составляющая . Высота, на которую поднимется снаряд за время τ, 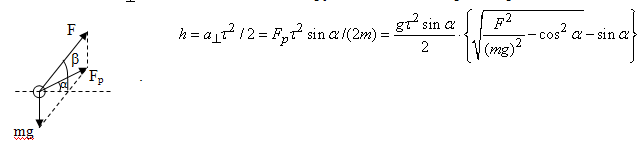
Задача 2. На рисунке показан цикл, совершаемый над идеальным газом, причем 1-2 – 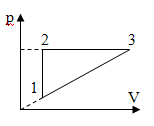 изохорный, 2-3 – изобарный процессы. Температура газа в точках 1 и 3 равны соответственно Т1 = 300 К и Т3 = 400 К. Найдите температуру газа в точке 2. Масса газа постоянна.
изохорный, 2-3 – изобарный процессы. Температура газа в точках 1 и 3 равны соответственно Т1 = 300 К и Т3 = 400 К. Найдите температуру газа в точке 2. Масса газа постоянна.
Решение: Указание: Записать уравнение Менделеева-Клайперона для трех состояний газа (1, 2 и 3), а также учесть, что p2 = p3, V1 = V2 и p3 = p1V3/V1. Ответ: .![]()
Задача 3. Толстостенный сосуд массой m = 1 кг изготовлен из материала, удельная теплоемкость которого с = 100 Дж/(кг·К). Сосуд содержит два моля одноатомного газа, объем которого V = 500 cм3 остается неизменным. Системе сообщают количество теплоты Q = 300 Дж. Найдите изменение давления газа. Универсальную газовую постоянную принять равной
R = 8,31 Дж/(моль·К).
Решение: Молярная теплоемкость одноатомного газа при постоянном объеме ![]() В результате сообщения сосуду с газом количество теплоты Q температура увеличилась на ΔТ и
В результате сообщения сосуду с газом количество теплоты Q температура увеличилась на ΔТ и ![]() . Изменение давления и температуры связаны соотношением
. Изменение давления и температуры связаны соотношением ![]() . Из последних двух уравнений находим:
. Из последних двух уравнений находим: ![]()
Задача 4. В схеме, показанной на рисунке, источник тока и амперметр поменяли местами. Какие 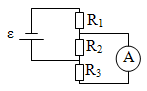 токи покажет амперметр в этих двух случаях? R1 = 20 Ом, R2 = 40 Ом, R3 = 60 Ом, ε = 10 В. Внутренним сопротивлением источника тока и амперметра пренебречь.
токи покажет амперметр в этих двух случаях? R1 = 20 Ом, R2 = 40 Ом, R3 = 60 Ом, ε = 10 В. Внутренним сопротивлением источника тока и амперметра пренебречь.
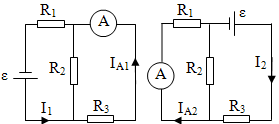 Решение: Схема первого подключения источника тока и амперметра показана на рис.1. Сила тока через источник в этом случае
Решение: Схема первого подключения источника тока и амперметра показана на рис.1. Сила тока через источник в этом случае ![]() а показания амперметра
а показания амперметра ![]() Во втором случае (рис.2) сила тока через источник
Во втором случае (рис.2) сила тока через источник ![]() , а сила тока через амперметр
, а сила тока через амперметр ![]() Таким образом показания амперметра в обоих случаях будут одинаковы. Ответ:
Таким образом показания амперметра в обоих случаях будут одинаковы. Ответ:![]()
Задача 5. На гладком горизонтальном столе лежит шар массой М, прикрепленной к пружине с  жесткостью к. В шар попадает пуля массой m, имеющая в момент удара скорость, направленную вдоль оси пружины (см.рис.). Считая удар абсолютно неупругим и пренебрегая массой пружины и сопротивлением воздуха, определите амплитуду и период колебаний шара.
жесткостью к. В шар попадает пуля массой m, имеющая в момент удара скорость, направленную вдоль оси пружины (см.рис.). Считая удар абсолютно неупругим и пренебрегая массой пружины и сопротивлением воздуха, определите амплитуду и период колебаний шара.
Решение: При соударении с шаром пуля сообщает ему 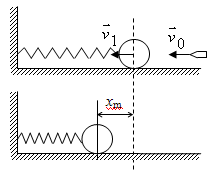 кинетическую энергию, вследствие чего шар приходит в движение и сжимает пружину. Пружина сжимается до тех пор, пока кинетическая энергия шара полностью не перейдет в потенциальную энергию деформации. В этот момент смещение шара от положения равновесия станет равно амплитудному значению. Дальше процесс пойдет в обратном порядке. Возвращающая сила упругости F, приложенная к шару, всюду при этом пропорциональна смещению x, и колебания шара будут гармоническими.
кинетическую энергию, вследствие чего шар приходит в движение и сжимает пружину. Пружина сжимается до тех пор, пока кинетическая энергия шара полностью не перейдет в потенциальную энергию деформации. В этот момент смещение шара от положения равновесия станет равно амплитудному значению. Дальше процесс пойдет в обратном порядке. Возвращающая сила упругости F, приложенная к шару, всюду при этом пропорциональна смещению x, и колебания шара будут гармоническими.
Закон сохранения импульса для системы пуля – шар: ![]() где v1 — скорость шара с пулей после удара. Рассмотрим два состояния системы: первое – шар начинает двигаться со скоростью v1, пружина не деформирована, второе – пружина максимально деформирована, смещение шара достигло амплитудного значения xm. В первом случае энергия системы
где v1 — скорость шара с пулей после удара. Рассмотрим два состояния системы: первое – шар начинает двигаться со скоростью v1, пружина не деформирована, второе – пружина максимально деформирована, смещение шара достигло амплитудного значения xm. В первом случае энергия системы ![]() во втором
во втором ![]() Так как поверхность стола идеально гладкая и сопротивление воздуха ничтожно мало W1 = W2
Так как поверхность стола идеально гладкая и сопротивление воздуха ничтожно мало W1 = W2![]()
Решая совместно уравнения (1) и (2) получим: ![]() Для нахождения периода колебаний запишем уравнение второго закона Ньютона для шара с пулей:
Для нахождения периода колебаний запишем уравнение второго закона Ньютона для шара с пулей:
F = (m+M)ax, где F = —kx, а ax – ускорение шара. Шар совершает гармонические колебания, их можно представить как проекцию на ось ОХ точки, движущейся по окружности радиусом R с постоянной угловой скоростью ![]() , Т – период колебаний. Нормальное ускорение этой точки an = w2r . Проекция этого ускорения на ось ОХ: ax = — w2r. Знак минус, так как ускорение направлено в сторону противоположную смещению. Таким образом, получим
, Т – период колебаний. Нормальное ускорение этой точки an = w2r . Проекция этого ускорения на ось ОХ: ax = — w2r. Знак минус, так как ускорение направлено в сторону противоположную смещению. Таким образом, получим ![]()
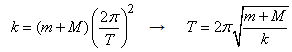
Ответ: