Задания по математике для 10 класса

1. Определите, при каких a уравнение имеет единственное решение.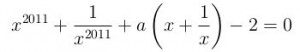 

Решение: Вместе с x корнем уравнения будет и 1/x. Поэтому в случае единственного решения получаем x = 1/x, откуда x = 1 или x = −1. Подставляя эти значения в исходное уравнение, получим a = 0 или a = −2. Проверяем. Если a = 0, единственность следует из неравенства 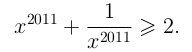 В случае a = −2 функция 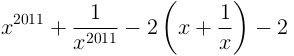отрицательна в точке x = 1 и положительна в точке x = 2. Поэтому исходное уравнение имеет, кроме x1 = −1, еще хотя бы один корень x2 ∈ (1, 2). Ответ: a = 0.

2. Решая задачу по геометрии, Костя нашел площадь, периметр и радиус вписанной окружности треугольника. Оказалось, что каждое из этих трех чисел удовлетворяет уравнению x² − 14x + 24 = 0. Докажите, что Костя ошибся.
Решение: Пусть стороны треугольника a ≤ b ≤ c, r — радиус вписанной окружности, h — высота, опущенная на c. Имеем цепочку очевидных неравенств: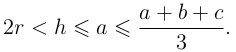 Поэтому отношение периметра к радиусу r всегда больше 6. Но корни Костиного уравнения 2 и 12.

3. Докажите, что уравнение 2(a + b + c) = ab + bc + ca + 3 имеет бесконечно много решений в натуральных числах a, b, c.
Решение:  Положим a = 1. Получим b + c = bc + 1, или (b − 1)(c − 1) = 0, откуда при b = 1, c — любое. В итоге для любого натурального n тройка (1, 1, n) является решением уравнения.

4. Существует ли треугольник ABC и точка O внутри него такие, что площади треугольников AOB, BOC, COA и ABC образуют
a) арифметическую прогрессию;
б) геометрическую прогрессию?
Решение:  Пусть площади треугольников AOB, BOC, COA и ABC равны S₁ , S₂ , S₃ и S соответственно. Справедливо равенство S₁ + S₂ + S₃ = S. В пункте а) получаем 3a + 3d = a + 3d, невозможно. В пункте б) получим b(1 + q + q²) = bq³. Существует положительное решение q0 уравнения 1 + q + q² = q³ . Проведем из произвольной точки O плоскости три луча, образующие друг с другом углы по 120^o , и отложим на них отрезки OH₁, OH₂ и OH₃ , равные 1, q₀ и q₀² соответственно. Прямые, перпендикулярные этим лучам в точках H₁ , H₂ и H₃ образуют стороны правильного треугольника ABC, а точка O удовлетворяет всем нужным требованиям. Ответ: а) не существует; б) существует.

5. Докажите для произвольного натурального числа n, что (2010n)! не делится на 2011ⁿ . Через (M)! обозначен факториал натурального числа M , т.е. произведение всех натуральных чисел от 1 до M : (M)! = 1 · 2 · 3 · . . . M.
Решение: 2011 — простое число. Поэтому, если (2010n)! делится на
2011k , то, расписывая (2010n)! = 1 · 2 · 3 · . . . 2010n, и выделяя сомножители, делящиеся на число 2011 и его степени, получим