Задания по математике для 11 класса

1. У Оли много одинаковых деревянных кубиков. Каждый день, кроме субботы и воскресенья, Оля берет новый кубик и раскрашивает каждую его грань в один из семи цветов радуги так, чтобы все грани имели разные цвета. Оля начинает окрашивать кубики 3 января 2011 года. Докажите, что 26 ноября 2011 года у неё найдутся два одинаково раскрашенных кубика.

Решение: 1. Подсчитаем количество способов раскрасить кубик. Выбрать 6 цветов для граней из 7-ми цветов радуги можно семью способами. Пусть мы выбрали цвета (a, b, c, d, e, f ). Фиксируем грань цвета a. Противоположная ей грань может быть окрашена пятью способами. Пусть цвет противоположной грани b. Поворачивая кубик, фиксируем тройку (a, c, b). Оставшиеся три цвета можно распределить 3 · 2 · 1 = 6 способами. Итого
7 · 5 · 6 = 210 способов. Трудовых будней в году не меньше чем [365/7] · 5 = 260. Оля не использовала не больше 40 будней, значит у нее не меньше 220 раскрашенных кубика. Следовательно, найдутся одинаковые.

2. Определите, при каких целых m уравнение 2(a + b + c) = ab + bc + ca + m

Решение: Так как ab + 1 ≥ a + b, bc + 1 ≥ b + c, ca + 1 ≥ c + a, то при m > 3
ab + bc + ca + m > ab + bc + ca + 3 ≥ 2(a + b + c),
и уравнение не имеет решений. В случае m ≤ 3 положим a = 1. Получим b + c = bc + m − 2, или (b − 1)(c − 1) = 3 − m. Полагая b = 2 получаем c = 4 − m. Ответ: при m ≤ 3.

3. Объем V правильного тетраэдра удовлетворяет неравенствам: 1812 < V < 2012. Выясните, существует ли точка внутри тетраэдра, расстояния от которой до граней тетраэдра образуют арифметическую прогрессию целых чисел.
Примечание. Объем тетраэдра V может быть вычислен по формуле: V = (hS)/3 , где h — высота тетраэдра, опущенная на основание площади S.

Решение:  Пусть длина ребра тетраэдра a, высота h. Тогда h =  Кроме того, используя разбиение тетаэдра на 4 тетраэдра с вершиной во внутренней точке O, и равенства для объемов, получим, что сумма расстояний от O до граней тетраэдра равна h. Для точки из условия задачи получим (a)+(a + d) + (a + 2d) + (a + 3d) = 4a + 6d = h. В итоге получим
систему: 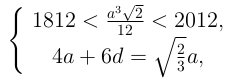с целыми a и d. Далее,  и, следовательно, Получаем неравенства 

Используя неравенства 1, 7 < √3 < 1, 8, получаем  Поэтому (∗) невозможно при целых a и d. Ответ: не существует.

4. К двузначному числу xy приписали справа это же число 2012 раз: xyxy . . . xy. Докажите, что получившееся 4026-значное число не может быть полным квадратом.

Решение: Число A из задачи делится на 11, так как 2013x − 2013y
делится на 11. Покажем, что оно не делится на 121.
A = xy · 101010 . . . 0101.
Число справа, состоящее из 2013 единиц и 2012 нулей, можно представить в виде
1010 . . . 01 · 100 . . . 0100 . . . 0 . . . . . . 100 . . . 01,
где в первом числе участвуют 11 единиц, а второе состоит из блоков 100 . . . 0 длины 22 и свободной единицы в конце. Во втором числе всего 183 единицы, все они стоят на четных местах, следовательно второе число не делится на 11. Поделим столбиком первое число на 11, получим
1010 . . . 01 = 11 · 9182736455463728191.
Второе число не делится на 11 по признаку (мешает единичка в конце). Поэтому, если A делится на 121, то xy делится на 11. Применяя к разложению
A = xy · 101010 . . . 0101,
признаки делимости на 3 и 9, получаем, что xy может быть лишь 33 или 66. Но квадрат не может оканчиваться на цифру 3, и не может оканчиваться на 66 (из-за делимости на 4).

5. Докажите, что для любых положительных чисел x и y, меньших единицы, существует треугольник со сторонами x^y , y^x , 1. Может ли такой треугольник быть тупоугольным?

Решение: Докажем неравенство  из которого сразу следует неравенство треугольника: 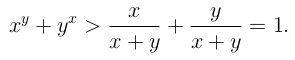 Неравенство (∗) перепишем в виде  или, равносильно, 

В справедливости последнего неравенства убеждаемся, сравнивая линейную функцию f (y) = 1 + ay и показательную g(y) = a^y в точках y = 0 и y = 1 (используем выпуклость g(y), но можно и просто исследовать разность f (y) − g(y)).

Тупоугольный треугольник с такими сторонами существует, например, при x = y = 1/3.