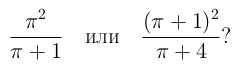Задания по математике для 8 класса
1. Определите, какое из чисел больше:
Примечание. π — отношение длины окружности к ее диаметру, π ≈ 3, 14.
Решение: Достаточно сравнить числа π2 (π + 4) и (π + 1)3 , или, равносильно, π2 и 3π + 1. Оценивая число π, получим 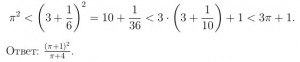
2. Цифры натурального числа A возрастают (слева направо), и A делится на 11. Докажите, что A не делится на 101.
Решение: От противного, пусть существуют числа из возрастающих цифр, делящиеся на 11 и 101. Из всех таких чисел выберем наименьшее число A. Тогда A делится на 1111 = 11 · 101. Вычитая из A число 11110 . . . 0 с таким же количеством цифр, что и у A, получаем число B < A со всеми интересующими нас свойствами. Получаем противоречие с минимальностью A.
Здесь ты найдешь уроки, исследования, интересные факты и вдохновение для творчества.
3. Докажите, что yравнение 2(x + y + z) = xy + yz + zx + 2011 не имеет решений в натуральных числах x, y, z.
Решение: xy + 1 ≥ x + y, так как (x − 1)(y − 1) ≥ 0. Аналогично
yz + 1 ≥ y+z и zx + 1 ≥ z + x.
Складывая эти три неравенства, получим
xy + yz + zx + 3 ≥ (x + y) + (y + z) + (z + x), откуда
xy + yz + zx + 2011 > 2(x + y + z).
4. Определите, какая цифра стоит на 2011-ом месте в последовательности
1223334444 . . . (число n приписывается ровно n раз).
Решение: Однозначные числа занимают 1 + 2 + 3 + · · · + 9 = 45 позиций. Двузначные числа от 10 до a9 занимают 2·(10+11+· · ·+a8+a9) = 2·(100+45+200+45+· · ·++a00+45) позиций. Последовательно складывая, получаем, что после выписывания всех чисел от 1 до 39 (последнее 39 раз), будут заняты 45 + 2 · (145 + 245 + 345) = 1515 позиции. Добавляем последовательно 2 · 40, 2 · 41, 2 · 42, 2 · 43, 2 · 44, получаем 1935 позиций. Приписывая 38 раз число 45, получаем на 2011-ой позиции цифру 5. Ответ: 5.
5. На стороне CD прямоугольника ABCD во внешнюю сторону построен правильный треугольник CDE. Оказалось, что радиус окружности, описанной около треугольника ABE, совпадает с длиной стороны AB. Докажите, что ABCD квадрат.
Решение: Пусть O — центр окружности. Тогда треугольник AOB правильный и равен треугольнику DEC. Так как AB║DC, то OB║EC, и OBCE — параллелограмм. Поэтому BC = OE = R = AB.