Задания по физике для 11 класса
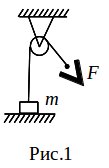 Задача 1. Через неподвижный блок (рис. 1) перекинута легкая веревка, к концу которой прикреплен груз массой m = 9 кг. Для поднятия груза с поверхности земли на высоту Н1 = 4 м за время t = 6 с надо тянуть веревку с постоянной силой F. На какую величину потребуется увеличить силу F, чтобы поднять груз с поверхности земли за то же время на высоту Н2 = 6 м? Массой блока и трением в его оси пренебречь.
Задача 1. Через неподвижный блок (рис. 1) перекинута легкая веревка, к концу которой прикреплен груз массой m = 9 кг. Для поднятия груза с поверхности земли на высоту Н1 = 4 м за время t = 6 с надо тянуть веревку с постоянной силой F. На какую величину потребуется увеличить силу F, чтобы поднять груз с поверхности земли за то же время на высоту Н2 = 6 м? Массой блока и трением в его оси пренебречь.
Решение: На груз действуют две силы: сила тяжести и сила натяжения нити, равная F. Под действием этих сил груз движется равноускоренно с ускорением a1 = (F — mg) / m. С другой стороны, при равноускоренном движении пройденный путь H1 = a1t2 / 2 и a1 = 2H1 / t2. Таким образом, имеем 2H1 / t2 = (F — mg) / m. Во втором случае сила натяжения веревки равна F + ΔF, а уравнение для ускорения a2 выглядит следующим образом: a2 = 2H2 / t2 = (F + ΔF — mg) / m. Вычитая a1 из a2, получаем 2(H2 — H1) / t2 = ΔF / m. Ответ: ΔF = 2m(H2-H1)/t2 = 1H
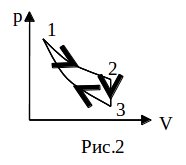 Задача 2. КПД тепловой машины, работающей по циклу (рис. 2), состоящему из изотермы 1-2, изохоры 2-3 и адиабатического процесса 3-1, равен η, а разность максимальной и минимальной температур газа в цикле равна ΔТ. Найдите работу, совершенную v молями одноатомного идеального газа в изотермическом процессе.
Задача 2. КПД тепловой машины, работающей по циклу (рис. 2), состоящему из изотермы 1-2, изохоры 2-3 и адиабатического процесса 3-1, равен η, а разность максимальной и минимальной температур газа в цикле равна ΔТ. Найдите работу, совершенную v молями одноатомного идеального газа в изотермическом процессе.
Решение: При изотермическом расширении газа (процесс 1→2) внутренняя энергия газа не изменяется и подведенное тепло Q12 равно работе А12, совершенной газом. При изохорическом охлаждении (процесс 2→3) изменение внутренней энергии ΔU23 = vcVΔT, где cV = 3/2R – молярная теплоемкость одноатомного идеального газа при постоянном объеме. В адиабатическом процессе 3→1 теплообмен газа с окружающей средой отсутствует, т.е. A31 = — ΔU31 = 0. Так как температура в точках 1 и 2 одинакова, то ΔU31 = — ΔU23 = vcVΔT. Поэтому A31 = — ΔU31 = -vcVΔT. Коэффициент полезного действия η = (A12 + A31) / Q12 = [A12 — (3vRΔT) / 2] / A12. Откуда получаем ответ:A12 = (3vRΔT) / 2(1 — η).

Здесь ты найдешь уроки, исследования, интересные факты и вдохновение для творчества.
Задача 3. На наклонной плоскости, составляющей угол α с горизонтальной поверхностью, находится маленькая шайба с прикрепленной к ней нитью (рис 3). Другой конец нити закреплен в некоторой точке наклонной плоскости. Если шайбу отклонить (при натянутой нити) от положения равновесия на малый угол φ0 и отпустить (без начальной скорости), то в процессе колебаний максимальный угол отклонения шайбы в противоположном направлении будет равен φ1 (φ1 < φ0). Найдите коэффициент трения шайбы о плоскость. Размерами шайбы пренебречь, силу трения считать не зависящей от скорости.
Решение: На рис. показаны начальное и конечное положения шайбы при ее движении по плоскости. Путь, пройденный шайбой, S = l(φ0 + φ1) , где l – длина нити. Сила трения, действующая на движущуюся шайбу, F = μmgcosα, где μ – искомый коэффициент трения. Работа силы трения A=F·S. Изменение у координаты шайбы Δy = l(cosφ1 — φ0), а изменение высоты Δh= Δysinα (см.рис.). Уменьшение потенциальной энергии шайбы П0 — П1 = -mg Δh равно работе силы трения, поэтому mgl(cosφ1 — φ0)sinα=-μmgl(φ0 + φ1)·cosα. Из последнего уравнения получаем 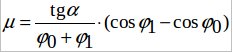 . Известно, что cos φ1 = 1 — 2sin2 (φ0 / 2) и cos φ0 = 1 — 2sin2 (φ0 / 2). Для малых углов sin(φ1 / 2) = φ1 / 2 и sin(φ0 / 2) = φ0 / 2, поэтому
. Известно, что cos φ1 = 1 — 2sin2 (φ0 / 2) и cos φ0 = 1 — 2sin2 (φ0 / 2). Для малых углов sin(φ1 / 2) = φ1 / 2 и sin(φ0 / 2) = φ0 / 2, поэтому ![]()
Подставляя выражение для разницы косинусов в выражение для коэффициента трения, получаем μ = (φ0 — φ1) · tgα /2.
Задача 4. Определите индуктивность катушки, если при постоянном изменении в ней тока от J0 = 5 А до J = 10 А за время τ = 0,1 с возникает ЭДС самоиндукции ε = 20 В.
Решение: ЭДС самоиндукции ![]() , откуда находим индуктивность катушки
, откуда находим индуктивность катушки ![]() Гн.
Гн.
Задача 5. После того, как конденсатор, заряженный до разности потенциалов U1 = 500 В, соединили параллельно с незаряженным конденсатором емкостью С2 = 4 мкФ, между обкладками конденсатора установилась разность потенциалов U2 = 100 В. Чему равна емкость первого конденсатора?
Решение: Обозначим емкость первого конденсатора через С1. Тогда заряд на нем до подсоединения второго конденсатора q = C1U1. Суммарный заряд на конденсаторах при параллельном подсоединении к первому конденсатору второго не изменится, т.е. q = C1U1 = C1U1 + C2U2. Откуда следует ответ: ![]() Ф.
Ф.
