Задания по физике для 9 класса
Задача 1. Капли жидкости отрываются из капельницы через одинаковые неизвестные интервалы времени и падают на движущуюся с постоянной скоростью v0 ленту конвейера. В распоряжении экспериментатора имелась только линейка. Имея возможность изменять высоту h капельницы над лентой конвейера, он определил ускорение свободного падения. Как это он сделал?
Решение: Высота падения h капли связана со временем падения t соотношением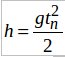 Расстояние между каплями на ленте конвейера Δl =v0 · t0 Выбирая высоту h так, чтобы tn = t0 (это означает, что вторая капля отрывается в момент приземления первой) получаем:
Расстояние между каплями на ленте конвейера Δl =v0 · t0 Выбирая высоту h так, чтобы tn = t0 (это означает, что вторая капля отрывается в момент приземления первой) получаем: 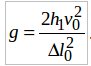 .
.
Задача 2. Аэростат массой m = 250 кг начал опускаться с ускорением
а = 0,2 м/сек². Определить массу балласта, который следует сбросить за борт, чтобы аэростат получил такое же ускорение вверх. Сопротивлением воздуха пренебречь.
Здесь ты найдешь уроки, исследования, интересные факты и вдохновение для творчества.
Решение: после сброса балласта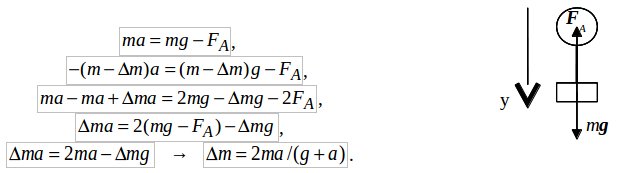
Задача 3. Определить удельную теплоту плавления льда, если известна удельная теплоемкость воды. Для определения удельной теплоты плавления льда дан металлический стакан, электроплитка и секундомер. К сожалению, в лаборатории не оказалось термометра.
Решение: Время, требуемое для расплавления льда τ1, если не учитывать теплообмен с окружающей средой 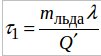 и время τ2, необходимое для нагревания полученной изо льда воды от 0°С до 100ºС
и время τ2, необходимое для нагревания полученной изо льда воды от 0°С до 100ºС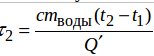
Из формул следует 
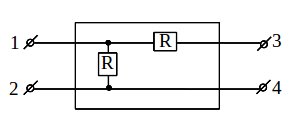
Задача 4. Дан черный ящик (см. рис.). Если подать напряжение U0 на клеммы 1-2, то с клемм 3-4 снимается напряжение U0. Если подать напряжение U0 на клеммы 3-4, то с клемм 1-2 снимается напряжение U0/2. Какая схема в черном ящике?
Задача 5. К коромыслу весов подвешены два груза равной массы. Если один из грузов поместить в жидкость плотности ρ1, а другой в жидкость плотности ρ2, то равновесие сохраняется. Найдите отношение плотности грузов.
Решение: Обозначим плотности грузов через p1′ и p2′, p′1,2=m/V1,2, где V1,2 объемы грузов. Из условия равновесия: 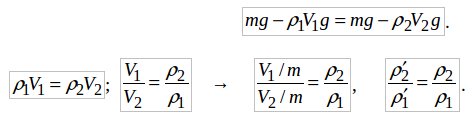
Плотности грузов относятся как плотности жидкостей.