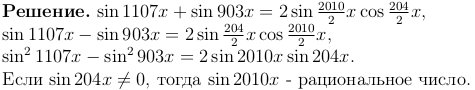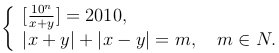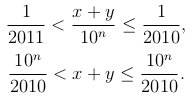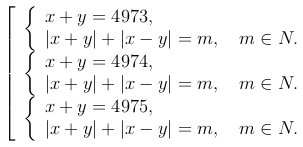Математика. 11 класс

Задача 1. Для некоторого числа x sin 204x, sin 903x, sin 1107x — рациональные отличные от нуля числа. Доказать, что sin 2010x — рациональное число.

Задача 2. Окружность, проходящая через середины медиан прямоугольного треугольника, касается его гипотенузы. Найдите углы этого треугольника.

Задача 3. Пусть P (x) — приведенный квадратный трехчлен, дискриминант которого
равен D. Известно, что неравенство P (x) < 0 имеет более 42 целых решений. Сколько целых решений имеет неравенство P (x − √D) + P (x) + P (x + √D) < 2010.

Решение.P (x) = x² + px + q, D = p² − 4q. |x₁ − x₂| = √D.

|x₂ − x₁ | ≥ 41, √D ≥ 41, −D ≤ −1681.

Рассмотрим выражение
P (x − √D) + P (x) + P (x + √D) = 3x² + 3px + 2p² − 5q,

3x² + 3px + 2p² − 5q − 2010 < 0,
D₁ = 9p² − 12(2p² − 5q − 2010) = 12 · 2010 − 15D < 12 · 2010 − 15 · 1681 = 24120 − 25215 < 0.
Следовательно, неравенство P (x − √D) + P (x) + P (x + √D) < 2010 не имеет решений.

Ответ. Решений нет.

Задача 4. Радиусы двух окружностей соответственно 1 и 3, расстояние между центрами окружностей — 10. Найти геометрическое место середин отрезков, соединяющих точки данных окружностей.

Решение. Введем на плоскости систему координат так, чтобы центры окружностей
лежали на оси абсцисс симметрично относительно начала координат. Параметрические уравнения окружностей будут иметь вид: x₁ = −5+cos t₁ , y₁ = sin t₁ и x₂ = 5+3 cos t₂, y₂ = 3 sin t₂ соответственно. Для точки (x, y), являющейся серединой отрезка, соединяющего точки (x₁, y₁ ) и (x₂, y₂), имеем:
(x, y) = ½(cos t₁ + 3 cos t₂ , sin t₁ + 3 sin t₂).
Если зафиксировать t₂ , то с изменением t₁ от 0 до 2π точка (x, y) будет описывать окружность радиуса ½ . При изменении t₁ от 0 до 2π центр указанной окружности (3/2 cos t₂ , 3/2 sin t₂ ) в свою очередь будет двигаться по окружности радиуса ½ с центром в начале координат; окружность радиуса ½ будет при этом «заметать» кольцо с внутренним радиусом 3/2 − ½ = 1 и внешним радиусом 3/2 + ½ = 2.
Ответ. Геометрическое место точек представляет собой кольцо, центр которого есть середина отрезка, соединяющего центры окружностей, а внутренний и внешний радиусы равны соответственно 1 и 2.

Задача 5. Найти наименьшее натуральное n, при котором система имеет единственное решение, если известно, что x + y — целое. Чему равно m.

Решение. Рассмотрим первое уравнение системы. По определению целой части числа имеем:

Из последнего неравенства получаем, что наименьшее натуральное n при котором x + y является целым — n = 7, тогда

Заметим, что при m = 4973 первая система совокупности имеет единственное решение, вторая и третья системы решений не имеют. При m = 4974 первая система совокупности имеет два решения, вторая одно решение, третья не имеет решений. При m = 4975 первая и вторая системы совокупности имеют два решения, третья система одно решение.
Ответ. n = 7, m = 4973.