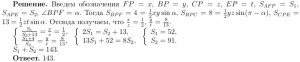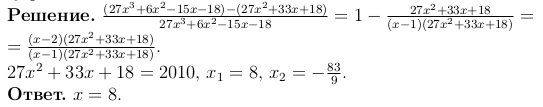Математика. 9 класс

Задача 1. На доске написаны многочлены P₁ = x² + 2, P₂ = x + 1. На доску дописываются многочлены, являющиеся суммой, разностью или произведением уже записанных многочленов. Может ли после нескольких дописываний на доске появиться многочлен Q(x) = 20x² + 10x.

Решение. P₁ (−1) = 3, P₂ (−1) = 0. Значит, все появляющиеся на доске многочлены таковы, что их значения в точке x = −1 делятся на 3. Q( − 1) = 10, следовательно, многочлен Q(x) таковым не является. Ответ. Не может.

Задача 2. Внутри треугольника ABC взяли точку P. Прямые BP и CP пересекают стороны треугольника ABC в точках E и F соответственно. Найдите площадь четырехугольника AFPE, если S_BPF = 4, S_BPC = 8, S_CPE = 13.

Задача 3. В школе работает 6 кружков. Каждый из 20 учеников класса может посещать любое количество кружков — от 0 до 6. Верно ли, что обязательно найдутся такие 5 учеников и такие 2 кружка, что все пятеро либо посещают оба кружка, либо не посещают ни один из этих двух кружков?

Решение. Пусть каждый ученик посещает ровно 3 кружка, причем у каждого набор 3 кружков отличен от других. (Это возможно, т.к. C₆³ = 20.) Тогда и наборы непосещаемых кружков также будут разными у разных учеников. Если бы некоторые 5 человек посещали одновременно какие-нибудь два кружка, тогда из оставшихся 4 кружков по крайней мере один пришлось бы посещать одновременно двум ученикам (принцип Дирихле), что приводит к противоречию. Ответ: нет.

Задача 4. Наугад выбрано 2010- значное число A, делящееся на 9. S(A) — сумма цифр этого числа. Найдите S(S(S(A))).

Решение. Введем обозначение
a = S(A) ≤ 9 · 2011 = 18099,
т.к. каждая цифра числа не превышает 9, то число a неболее чем пятизначное число.
b = S(a) ≤ 5 · 9 = 45,
b — двузначное число, делящееся на 9.
c = S(b) ≤ 2 · 9 = 18,
c — делится на 9, следовательно c = 9, 18.
Если c = 18, то b = 99, но b ≤ 45.
Если c = 9, то b = 18, a = 1089.
Ответ. 9.

Задача 5. При каких целых x дробь можно сократить на 2010. Чему равно A.