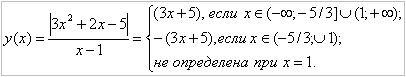Олимпиадные задания по математике для 10 класса
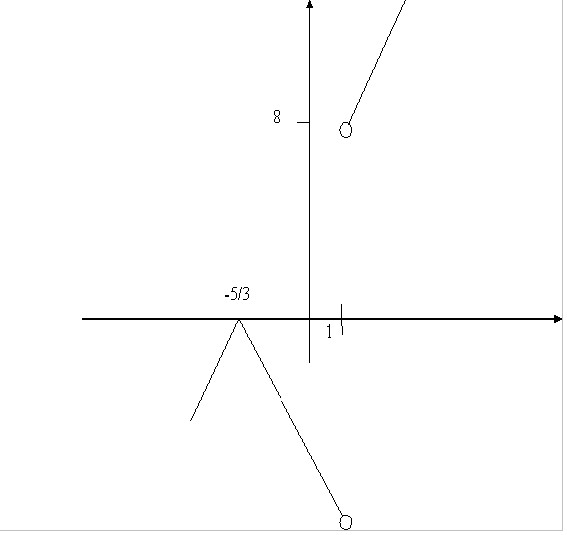
1. Постройте эскиз графика функции: ![]()
2. При каком значении параметра a значение выражения x1² + x2² будет наименьшим, если x1 и x2 — корни уравнения x²+ax+a-2=0?
Здесь ты найдешь уроки, исследования, интересные факты и вдохновение для творчества.
Решение:
По т. Виета: x₁+x₂=−a, x₁⋅x₂=a−2⇒x²₁+x²₂=(x₁+x₂)² — 2х₁х₂ =a²−2a+4=f(a).Нам надо найти аmin для функции f(a), при котором уравнение x²+ax+a−2=0 имеет корни, т.е. D=a²−4a+8>0, но это верно при всех a∈R, поэтому просто ищем минимум f(a).f(a)=(a−1)²+3≥3⇒amin=1.
3. Решите уравнение x2 -2х + у2 – 10 у + 26 = 0
Ответ: (1;5)
4. Решите уравнение (х — 1) (х — 3) ( х – 5) (х – 7) = 945
Ответ: -1; 9
5. Найдите периметр равнобедренной трапеции, у которой меньшее основание равно 8, острый угол 45° и высота равна 2 √2.
Ответ: 4 √2 + 2
6. В одном магазине молоко подешевело на 40%, а в другом – сначала на 20%, а затем еще на 25%. Первоначальная цена на молоко в каждом из магазинов была одна и та же. Где молоко стало стоить дешевле?
Решение: Пусть х рублей первоначальная цена молока. В первом магазине цена уменьшилась на 40%, то есть составила 0,6х рублей. Во втором магазине после первого понижения цена была 0,8х рублей, а после второго — 0,75(0,8х)=0,6х. Таким образом, молоко в каждом из магазинов вновь стоит одинаково.