Олимпиадные задания по физике для 7 классов
1. Строение кристалла некоторого металла схематически показано на рисунке. Атомы находятся в вершинах кубиков и образуют кубическую кристаллическую решётку. Известно, что плотность этого металла равна ρ = 7900 кг/м3, а масса одного атома m0 9,3 · 10−26 кг. Найдите объём V0 одного кубика — элементарной ячейки данной кристаллической решётки.
Решение: Проведём плоскости перпендикулярно серединам рёбер кубиков. В результате кристалл окажется разделённым на кубики, в каждом из которых находится по одному атому. Пусть кристалл имеет объём V и содержит N атомов. Тогда плотность металла 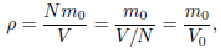
где V0 = V/N. — объём, приходящийся на один атом, то есть искомый объём элементарной ячейки кристаллической решётки. Отсюда, ответ: ![]()
2. После того, как автобус проехал первую половину пути, он попал в дорожную пробку. В результате его средняя скорость на второй половине пути в 8 раз меньше, чем на первой. Средняя скорость автобуса на всем пути равна 16 км/ч. Определите скорость автобуса на второй половине пути.
Здесь ты найдешь уроки, исследования, интересные факты и вдохновение для творчества.
Решение: Пусть Vср – средняя скорость движения на всем пути S, а t1, t2, V1 и V2 время и скорости автобуса на первой и второй половинах пути соответственно. Все время движения автобуса равно t = t1+ t2. По условию задачи t1=(S/2)/8V2 = S/16V2 и t2=(S/2)/V2 = S/2V2. Используя эти выражения, находим время движения автобуса t = + = .(3б) Из формулы = определяем время t = S/16V2 + S/2V2 = 9S/16V2. Из формулы Vср = s/t определяем время t= s/Vср. Таким образом ответ 9 км/ч.
3. Ученик измерил плотность деревянного бруска, покрытого краской, и она оказалась равной ρ= 600 кг/м³. Но на самом деле брусок состоит из двух частей, равных по массе, плотность одной из которых в два раза больше плотности другой. Найдите плотности обеих частей бруска. Массой краски можно пренебречь.
Решение:
Пусть m — масса каждой из частей бруска, p1и p2= p1/2 — их плотности. Тогда части бруска имеют объёмы m/p1и 2m/p1, а весь брусок массу 2m и объём 3m/p1. Средняя плотность бруска p =2m/3m/p1=2p1/3
Отсюда находим плотности частей бруска: p1 = 3p/2 = 900 кг/м3 ,
p2 = 3p/4 = 450 кг/м3.
4. Стальная Эйфелева башня в Париже высотой 300 м имеет массу 7200 т. Какую массу имела бы точная модель этой башни высотой 30 см?
Решение: Размеры модели Эйфелевой башни меньше в 300/0.3 = 1000 раз. Поэтому объем каждой детали будет уменьшенным в 1000·1000·1000=109 раз, а так как масса пропорциональна объему, то масса модели будет равна m = M/109 = 0,0072 кг.
5. Два спортсмена одновременно стартуют в противоположных направлениях из одной точки замкнутой беговой дорожки стадиона и к моменту встречи пробегают – один 160 м, а другой 240 м. При старте в одном направлении более быстрый спортсмен дает 100 м форы более медленному. Через сколько метров от точки старта он догонит соперника?
Решение: Отношение скоростей спортсменов равно отношению расстояний, пройденных в первом забеге, т.е. 240/160 = 3/2. Во втором забеге расстояния, пройденные ими с момента старта быстрого спортсмена, также относятся как 3:2. Это будет в том случае, когда быстрый спортсмен пробежит от старта 300 м, а медленный за это время 300 – 100 = 200 м.
Ответ: Более быстрый спортсмен догонит соперника через 300 м от точки старта.
