Экономика. 9-11 классы. Задачи

Задача 1.
Государство собирается ввести на рынке импортных автомобилей потоварный налог. С помощью налога нужно собрать не менее 16 млн. руб. Экономисты правительства оценили для данного рынка кривую Лаффера при введении потоварного налога:

T = 10000t — 1000t²,
где t — ставка налога (в тыс. руб.), а Т — общая сумма налоговых поступлений (также в тыс. руб.). На сколько процентов государству удастся максимально сократить объем продаж импортных автомобилей?

Решение: Найдем, какие ставки налога обеспечат как нужную сумму:

T = 10000t — 1000t² = 0 →t₁ = 0, t₂ = 10.

Однако, максимум Т достигается при T′ = 10000 — 2 *1000t = 0 →t_max = 5 →T_max = 25000.

Свыше 16 млн. руб. будет собрано при T = 10000t — 1000t² ≥ 16000 →t² +10t -16 = 0 →t₁ = 2, t₂ = 8.

Поскольку государство стремится минимизировать объем продаж импортных автомобилей, значит, оно установит максимальную налоговую ставку из всех подходящих: t = 8.
Для того чтобы найти изменение рыночного объема, вспомним, что сумма налоговых поступлений при введении потоварного налога равна tQ, где Q(t) — равновесный объем, который установится на рынке при введении налога по ставке t.

T = 10000t — 1000t² = t * Q(t) →Q(t) = 10000 — 1000t,

До налогообложения рыночный объем равнялся Q(0), то есть 10000. После введения налога рыночный объем составит: Q (8) = 2000, Объем продаж сократится на 80%.

Задача 2. Ферма выращивает картофель на корм собственному скоту, остатки которого продает на рынке по цене 20 тыс. руб. за т, выручку от которых тратит на покупку посевного материала. Функция издержек фермы на производство картофеля задается уравнением TC(Q)=(Q+2)². Столовая  покупает у фермы картофель, а также у других производителей иные продукты по цене 10 тыс. руб. за т на общую сумму 100 тыс. руб. в месяц, производя горячие обеды. На производство одного обеда расходуется 1 кг картофеля и 0,5 кг иных продуктов. Какой объем картофеля расходуется фермой и столовой в месяц?

Решение: Пусть q_s — количество картофель, которое ферма производит для себя, а q_m— для продажи на рынок. Тогда Q = q_{s +} q_m, TC = (q_s+q_m+2)². Поскольку выручку ферма получает только от тех единиц продукции, которые проданы на рынок, TR = 20q_m. Так как всю прибыль она тратит на производство для себя, выполняется: 20q_m = (q_s+q_m+2)². При этом условии ферма максимизирует q_s:

Отсюда — ферма выращивает для собственных нужд 3 т. Столовая использует картофель (R) и другие продукты (G) в пропорции: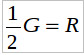 

Поскольку бюджетное ограничение столовой имеет вид 10G + 20R = 100, решая систему, получаем G = 5, R = 2,5 — столовая расходует в месяц 2,5 т картофеля и 5 т других продуктов.

Задача 3. Фирма является монополистом на рынке телевизоров. В краткосрочном периоде фирма использует единственный переменный фактор производства – труд, и закупает его на совершенно конкурентном рынке. Известно, что в точке оптимума коэффициент эластичности выручки данной фирмы по выпуску составил 0,2, а работники фирмы в количестве 10 человек в среднем производят 1000 телевизоров, и фирме для достижения оптимума необходимо уволить трех работников, причем производительность труда каждого нового работника на 5% ниже ранее нанятого. Сколько телевизоров может купить рабочий этой фирмы на одну зарплату?

Решение: Запишем условие оптимума фирмы-монополиста: MR * MP_L = w. Разделим обе части уравнения на рыночную цену товара (р): 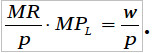Но эластичность выручки по выпуску как раз равна: Необходимо найти MP_L  в точке оптимума. Запишем условия: 

где n – количество работников.
При n=10: 

Значит, 

Это и есть ответ на вопрос задачи: величина w/р как раз показывает реальную зарплату рабочего, выраженную в телевизорах.

Задача 4. На рисунке представлены графики средних переменных (AVC) и средних постоянных (АFС) издержек фирмы-монополиста. А также график спроса на его продукцию (D). Определите, какой объем выпуска должна выбрать фирма, чтобы максимизировать прибыль (минимизировать убытки)? Восстановите уравнение кривой спроса.

Решение: Определим функцию средних переменных издержек по графику:

(1) AVC = 0,5Q + 10.
Найдем выражение переменных издержек:
(2) VC = 0,5Q² + 10Q
Поскольку средние постоянные издержки равны:
Найдем функцию общих издержек:
(4) TC = 0,5Q² + 10Q + 750
Выражение средних постоянных издержек: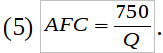
Для определения уравнения спроса найдем Q при AFC=75: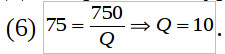 
Запишем уравнение спроса в общем виде (линейное):
(7) p = a — bQ
Из условия касания p(Q) и AC следует: 
Подставим Q=10 и р=AFC=75 в (7): 
Запишем условие максимума прибыли (минимума убытка): При этом максимизируется прибыль, поскольку: