Математика. 8 класс
Задача 1. Решите систему уравнений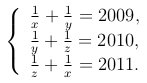
Решение: x = 1/1005 , y = 1/1004 , z = 1/1006 .
Задача 2. Сколько решений в натуральных числах имеет уравнение
xyz = 2009 · 2010 · 2011.
Решение. 2009 = 7² ·41, 2010 = 2·3·5·67, 2011 — простое. Тогда xyz = 2·3·5·7²·41·67·2011.
Ответ. 36 · 6 = 37 · 2 = 4374.
Здесь ты найдешь уроки, исследования, интересные факты и вдохновение для творчества.
Задача 3. Имена Иванова, Петрова, Семенова и Николаева — Иван, Петр, Семен и Николай, причем только у Николаева фамилия происходит от его же имени. Семенова зовут не Петром. Назовите фамилию и имя каждого.
Ответ. Иванов Петр, Петров Семен, Семенов Иван, Николаев Николай
Задача 4. На доске написаны числа 1, 2, …, 100. Разрешается стереть любые два числа a и b и вместо них написать число a + b − 1. Какое число может остаться на доске после выполнения 99 таких операций?
Решение. Обозначим через S сумму всех чисел, написанных на доске. Поскольку 1 + 100 = 2 + 99 = … = 50 + 51 = 101, вначале = 101 · 50 = 5050. Заметим, что на каждом шаге количество чмсел и сумма S уменьшается на 1. Поэтому после 99 таких операций на доске останется одно число равное S − 99 = 4951. Ответ. 4951.
Задача 5. Пусть S(n) — сумма цифр натурального числа n. Найдите все n, для которых n + S(n) + S(S(n)) = 2010.
Ответ. 2002+4+4 = 2010, 1978+25+7 = 2010, 1981+19+10 = 2010, 1984+22+4 = 2010.
