Математика

Олимпиадные задания по математике для 11 класса

1. Докажите, что произведение четырех последовательных целых чисел, сложенное с единицей, есть точный квадрат.

Решение: Пусть это 4 последовательных числа: n, n + 1, n + 2, n + 3. Тогда n (n + 1)(n + 2)(n + 3) + 1 = (n² + 3n)(n² + 3n + 2) + 1 = (n² + 3n)²+ 2(n² + 3n) + 1 = (n² + 3n + 1)².

2. Решите уравнение

Решение: Перенесем в левую часть и прибавим, и вычтем по cos⁸x. В результате полученное уравнение можно преобразовать к виду (sin4x – cos⁴x)² + cos²x(1 – cos⁶x) = 0, которое равносильно следующей системе: Решая второе уравнение и подставляя его решения в первое уравнение, в результате получим решение исходного уравнения . Ответ:

(далее…)

Задания по математике для 11 класса

1. У Оли много одинаковых деревянных кубиков. Каждый день, кроме субботы и воскресенья, Оля берет новый кубик и раскрашивает каждую его грань в один из семи цветов радуги так, чтобы все грани имели разные цвета. Оля начинает окрашивать кубики 3 января 2011 года. Докажите, что 26 ноября 2011 года у неё найдутся два одинаково раскрашенных кубика.

(далее…)

Задания по математике для 9 класса

1. Поверхность деревянного куба окрасили в красный цвет. После этого куб распили на 1000 одинаковых кубиков. Вычислите, сколько из этих кубиков имеют ровно две окрашенные грани.
Решение: Все такие кубики были на ребре, но не в вершинах куба.
Ребер 12, на каждом ребре 10 − 2 = 8 таких кубиков. Всего 12 · 8 = 96. Ответ: 96.

(далее…)

Задания по математике для 7 класса

1. Определите, какое из чисел больше:

(далее…)

Задания по математике для 8 класса

1. Определите, какое из чисел больше:

(далее…)

Задания по математике для 10 класса

1. Определите, при каких a уравнение имеет единственное решение. 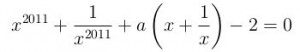(далее…)

Задания по математике 11 класс

1. Докажите равенство:

Ответ: Так как в обеих частях предполагаемого равенства стоят углы из первой четверти, достаточно доказать равенство их тангенсов. По формуле для тангенса суммы имеем: