Олимпиады
Литература. 8 класс
Тур I. Комплексный анализ художественного текста.
И.С.Тургенев
ГОЛУБИ
Я стоял на вершине пологого холма; передо мною — то золотым, то посеребренным морем — раскинулась и пестрела спелая рожь.
Но не бегало зыби по этому морю; не струился душный воздух: назревала гроза великая. (далее…)
Литература. 9 класс
Тур I. Комплексный анализ художественного текста.
И.С.Тургенев
ДВА ЧЕТВЕРОСТИШИЯ
Существовал некогда город, жители которого до того страстно любили поэзию, что если проходило несколько недель и не появлялось новых прекрасных стихов, — они считали такой поэтический неурожай общественным бедствием. (далее…)
Литература. 10 класс
Тур I. Комплексный анализ художественного текста.
Николай Владимирович Станкевич
ТРИ ХУДОЖНИКА
Три художника, три брата работали вместе. Безмолвно каждый в своем углу покушался дать плоть прекрасному, мгновению своей жизни. Но у всех творило одно могучее чувство, одна мысль облекалась в красоту, один дух парил над тремя избранными. Лучи заходящего солнца проникали в комнату… (далее…)
Литература. 11 класс
Тур I. Комплексный анализ художественного текста.
Андрей Белый
РЕВУН
Мы сидели на террасе у провала. Перед нами хребты причудливых гор торчали безысходными изломами. Были покрыты верхи их пятнами грязного льда.
Сбоку была страна скорбящих молений. Было царство неведомых могил. Железная часовня глухо порывалась в пространство, застывая под кипарисами. Два серебряных ребенка с очами, полными слез, тяжелели на кровле. Над ними ненастье рвало кипарисы. (далее…)
Математика. 8 класс
Задача 1. Решите систему уравнений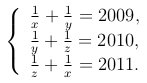
Решение: x = 1/1005 , y = 1/1004 , z = 1/1006 . (далее…)
Математика. 9 класс
Задача 1. На доске написаны многочлены P1 = x² + 2, P2 = x + 1. На доску дописываются многочлены, являющиеся суммой, разностью или произведением уже записанных многочленов. Может ли после нескольких дописываний на доске появиться многочлен Q(x) = 20x² + 10x.
Решение. P1 (−1) = 3, P2 (−1) = 0. Значит, все появляющиеся на доске многочлены таковы, что их значения в точке x = −1 делятся на 3. Q( − 1) = 10, следовательно, многочлен Q(x) таковым не является. Ответ. Не может.
Математика. 10 класс
Задача 1. Центры вписанной и описанной окружностей треугольника симметричны относительно одной из его сторон. Найдите углы треугольника.
Указание. Так как центр описанной окружности лежит вне треугольника, значит треугольник тупоугольный. Рассмотрим треугольник ABC с тупым углом A. O -центр описанной около треугольника окружности, O1 -центр вписанной в треугольник окружности. BC — сторона симметрии, K — точка симметрии. ∠C = α. Воспользоваться свойствами вписанных в окружность углов.
Ответ. 36º , 36º , 108º. (далее…)
Математика. 11 класс
Задача 1. Для некоторого числа x sin 204x, sin 903x, sin 1107x — рациональные отличные от нуля числа. Доказать, что sin 2010x — рациональное число.
Обществознание. 10 класс
1. Качества человека, отличающим его от животного, является:
1) способность к продолжению рода;
2) умение защищаться от врагов;
3) умение находить пропитание и обустраивать жилье;
4) страх смерти. (далее…)
Обществознание. 11 класс
1. Что включают ученые в понятие человеческого знания?
1) результат познавательной деятельности человека;
2) деятельность, в результате которой создаются новое;
3) социальная потребность человека;
4) результат любой творческой деятельности человека. (далее…)