Физика
Олимпиадные задания по физике для 8 класса
1.Сплав золота и серебра массой 400 г имеет плотность 1, 4 · 104 кг/м³. Полагая объем сплава равным сумме объемов его составных частей, определите массу золота в сплаве.
Решение: Масса сплава всегда равна сумме масс его составных частей: mсп = mc + mз. По условию задачи, объем сплава равен сумме объемов его составных частей: Vсп = Vc + Vз. Из формулы для плотности p=m/V следует, что V=m/p.
Подставляя выражение для объемов в последнюю формулу и выражая массу серебра через массу сплава и массу золота, получаем: mс = mcп — mз и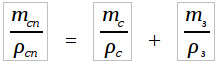 
(далее…)
Олимпиадные задания по физике для 10 класса
1.Из одной и той же точки вертикально вверх с интервалом времени Δt выброшены два шарика со скоростью V. Шарики движутся по одной прямой в поле силы тяжести. Через какое время после запуска второго шарика они столкнутся?
Решение. Запишем уравнение координаты первого и второго тела при движении вертикально вверх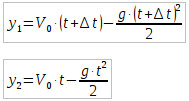 
. В точке пересечения траекторий координаты тел равны y1= y2. (2б) Поэтому приравниваем эти два уравнения и решаем относительно неизвестной величины t.
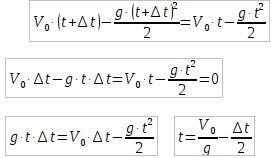(далее…)
Физика. 11 класс
Задача 1. На подставке лежит тело массы m, подвешенное на пружине жесткостью к. В начальный момент пружина не растянута. Подставку начинают опускать вниз с ускорением а. Через какое время подставка оторвется от тела?
Физика. 7 класс
Задача 1. Российский школьник Николай познакомился в интернете с английским школьником Майклом. В переписке Николай сообщил, что он пробегает 60 метров за 10 секунд, а Майкл ему ответил, что он за 10 секунд пробегает дистанцию длиной 2300 дюймов.
Кто из мальчиков на дистанции бежит быстрее?
Дюйм составляет 0,0254 от длины одного метра.
Физика. 8 класс
Задача 1. Поезд, вышедший в 12 часов дня из пункта А, движется со скоростью v1 = 60 км/час. Поезд, вышедший в 14 часов дня из пункта В, движется со скоростью v2 = 40 км/час навстречу первому поезду. В котором часу они встретятся, если расстояние АВ S = 420 км.
Физика. 9 класс
Задача 1. В копре для забивки свай груз равномерно поднимается в течение 5 сек со скоростью 98 см/с, после чего падает на сваю. Определите, сколько ударов делает груз в минуту.
Решение: Высота подъема 
,
Время падения 
Число ударов 
Физика. 10 класс
Задача 1. Вокруг планеты, имеющей форму шара радиусом R, по круговой орбите движется спутник.
Определите радиус орбиты спутника, считая известными ускорение свободного падения у поверхности планеты g и период обращения спутника Т.
Олимпиадные задания по физике для 7 классов
1. Строение кристалла некоторого металла схематически показано на рисунке. Атомы находятся в вершинах кубиков и образуют кубическую кристаллическую решётку. Известно, что плотность этого металла равна ρ = 7900 кг/м3, а масса одного атома m0 9,3 · 10−26 кг. Найдите объём V0 одного кубика — элементарной ячейки данной кристаллической решётки.
Решение: Проведём плоскости перпендикулярно серединам рёбер кубиков. В результате кристалл окажется разделённым на кубики, в каждом из которых находится по одному атому. Пусть кристалл имеет объём V и содержит N атомов. Тогда плотность металла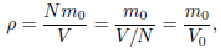 
где V0 = V/N. — объём, приходящийся на один атом, то есть искомый объём элементарной ячейки кристаллической решётки. Отсюда, ответ: 
Задания по физике для 11 класса
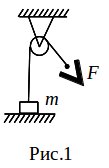Задача 1. Через неподвижный блок (рис. 1) перекинута легкая веревка, к концу которой прикреплен груз массой m = 9 кг. Для поднятия груза с поверхности земли на высоту Н1 = 4 м за время t = 6 с надо тянуть веревку с постоянной силой F. На какую величину потребуется увеличить силу F, чтобы поднять груз с поверхности земли за то же время на высоту Н2 = 6 м? Массой блока и трением в его оси пренебречь. (далее…)
Задания по физике для 10 класса
Задача 1. Двигатель запускаемого с земли реактивного снаряда массой m работает время τ, создавая постоянную по величине и направлению силу тяги F и обеспечивая прямолинейное движение снаряда под углом α к горизонту. Определите высоту, на которой прекращается работа двигателя. (далее…)